Perfect Polyominoes
While at Saint Ann's School, my 5th graders and I studied polyomino divisibility and played with problems of division and tiling. Polyominoes offer a beautiful blend of number theory and geometry, because they have size and shape with interesting restrictions. About a year after my move away from Brooklyn, I found myself pondering them again.
Imagining a geometric analog for perfect numbers, I defined the following: A perfect polyomino is one that may be reassembled as a sum of its proper factors. I enlisted the help of Justin Lanier, and together we came up with some interesting results, especially as they compare to the ancient search for perfect numbers. You can read an overview of our work, which we presented at the 2015 MOVES conference, at the National Museum of Mathematics. |
Overview of our work:
Perfect Polyominoes (MOVES proposal) Background: Polyomino Number Theory (I) Examples: The picture above shows the smallest known perfect polyomino of odd size. 
This "Q" is one of ten perfect hexomino configurations.
|
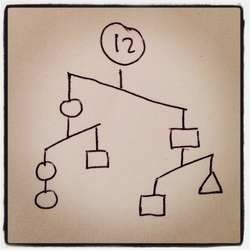
Imbalance Puzzles
Puzzle: Order the three types of shape by weight,
given that shapes of the same type weight the same.
|
See Sam Loyd's Puzzling Scales series for a classic example of the "balanced scale" genre. Inspired by them, I invented a new type of puzzle that uses unbalanced scales to give information about order and inequality.
I presented my puzzles at the 2013 MOVES Conference and published a handful of them. I hosted an online problem-writing contest, the results of which can be seen here, along with my original 15 puzzles. |
Problem set:
MOVES Conference handout Published: New York Times Numberplay The College Mathematics Journal MAA FOCUS Magazine Inspiration: Puzzling Scales by Sam Loyd |
My mathematical work can also be found on my old blog, Lost in Recursion.